主要内容来自于李沐老师的视频，shine-lee的博客，本文主要是以上内容的总结

Batch Normalization(BN批量归一化)

为什么需要BN(Batch Normalization)？

训练深度网络时，反向传播时每一层的参数会更新，在之后的前向传播时前面层的输出数据会不断变化，会导致后续的层需要不断适应这种变化（这种现象被称为内部协变量偏移），内部协变量偏移会导致训练困难和结果的不稳定
神经网络层数比较深时，反向传播的梯度由后向前计算，如果不做任何处理，那么后面的梯度变化会更加的敏感，前面的梯度变化不明显（因为一般情况下梯度会是n个较小的数相乘，乘到后面可能变化非常不明显，即梯度消失，反之则是梯度爆炸）
神经网络中前面的layer可能提取一些表面信息，后面的layer根据这些信息来提取高级信息，因此前面的层发生变化对后面的层影响较大，为了避免过于震荡，需要将学习率设置的足够小，会导致收敛比较慢的问题
Batch Normalization来解决这个问题

方法

输入为一个batch $B$ ，其中每个元素为 $x_i, i \in B$
获取小批量里面的均值 $\mu_B$ $μ_{B}$ 和方差 $\sigma_B$ $σ_{B}$
- $\mu_B = \frac{1}{|B|}\sum_{i\in B}{x_i}$ ， $\sigma^2_B = \frac{1}{|B|}\sum_{i\in B}{(x_i - \mu_B)^2}$
进行Standardization
- $\hat{x_i} = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$
- $\epsilon$ 是防止除零引入的极小量
进行Scale and shift
- $y_{i} = \gamma \hat{x_i} +\beta$
- 其中 $\gamma$ 为方差(scale参数)， $\beta$ 为均值(shift参数)，均为可学习的参数

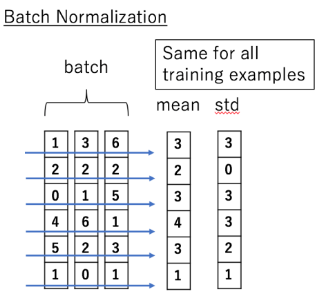
图片来自于李理的博客
在BN层中，不同层的输入 $x_i$ 和 $x_j$ 不存在信息交流

位置

一般放在全连接层和卷积层输出之后，激活函数之前，一般不用于激活函数之后
全连接层和卷积层的输入

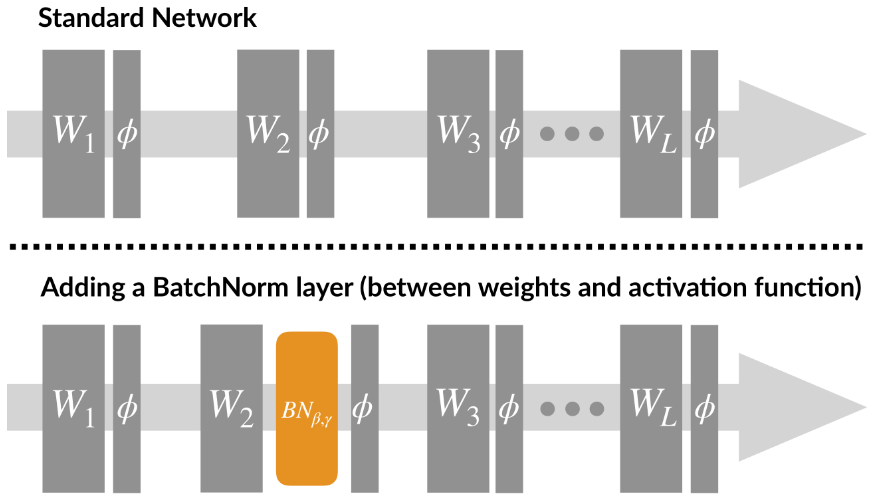
全连接层
- 在全连接层中，数据一般是二维的，通常表示为 [batch_size, features]
- 当应用Batch Normalization时，沿着batch维度（即第0维度）对每个特征进行标准化
- 即作用在特征维，将每组特征做BN
卷积层
- 在卷积层中，数据通常是四维的，表示为 [batch_size, channels, height, width]
- 一个卷积核产生一个feature map，一个feature map对应一对 $\gamma$ ， $\beta$
- 同一个batch同channel的feature map共享一对 $\gamma$ ， $\beta$ ，即卷积层有n个卷积核，那么有n对 $\gamma$ ， $\beta$ 参数
- 与全连接层不同，卷积层中的BN是沿着batch维度、高度和宽度对每个通道进行标准化
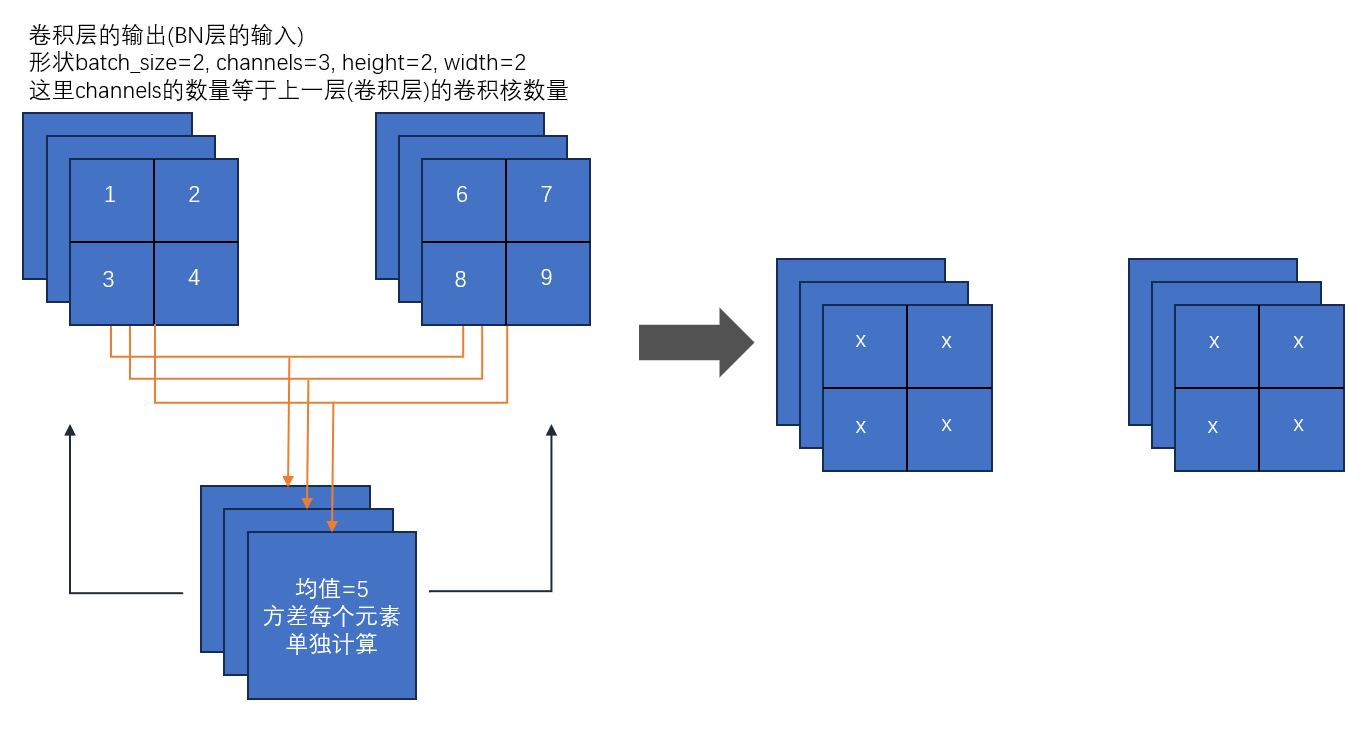
- 即作用在通道维，将每组channel做BN
主要使用在深层网络中

训练阶段

$\mu_B$ , $\sigma^2_B$ 对于一个batch来说都是固定的参数
只需要反向传播时更新 $\gamma$ 和 $\beta$ 即可

推理阶段

在这个阶段所有参数都是固定的，即 $\mu_B$ $μ_{B}$ ， $\sigma^2_B$ $σ_{B}^{2}$ ， $\gamma$ $γ$ ， $\beta$ $β$ 都是固定值
- $\mu_B$ ， $\sigma^2_B$ 在推理阶段可能只有1个值，可以采用训练收敛最后几个mini batch的 $\mu_B$ ， $\sigma^2_B$ 的期望作为推理阶段的 $\mu_B$ ， $\sigma^2_B$
- $\gamma$ ， $\beta$ 在训练结束后，两者收敛，直接采用收敛值即可

作用

Batch Normalization固定小批量中的均值和方差，然后学习出合适的偏移和缩放，来避免梯度的剧烈变化
可以加速收敛速度，但一般不改变模型精度，可以将学习率适当调大
对权重初始化和尺度不再敏感
抑制了梯度消失，可以使用sigmoid和tanh作为激活函数了
BN层具有某种正则作用，不太依赖dropout，减少过拟合

为什么BN层有效？

让损失函数更加平滑，有利于梯度下降，具体可以阅读论文
直觉上的解释，没有BN层的情况下，网络没法直接控制每层的输入分布，其分布由前面层的权重共同决定，网络想要调整分布的话，需要通过复杂的反向传播过程来调整前面每个权重的实现，BN层相当于将分布的均值和方差从权重中剥离出来，只需要调整 $\gamma$ ， $\beta$ 两个参数就可以调整每层的分布，让分布和权重的配合更加容易

适用场景

每个batch较大，数据分布比较接近
训练之前需要做好充分的shuffle

缺点

不适用于batch较小的情况，BN是对整个batch样本统计均值和方差
由于运行过程中需要统计每个batch的统计信息，因此不适用于动态网络结构和RNN

其他

没有scale and shift是否可行？
- 可以，但可能会导致网络的表达能力下降
- 浅层模型中，只需要模型适应数据分布即可，但是在深层模型中，需要输入分布和权重相互协调，强制把输入分布限制在zero mean unit variance并不见得最好，加入参数 $\beta$ 有利于分布和权重相互协调
BN层放在Relu前面还是后面？
- 原paper建议在Relu前，因为Relu输出非负，不能近似为高斯分布
- 但是也有其他研究说明前后差距不大

code
全连接层

import torch

class BatchNormalizationManual:
    def __init__(self, num_features, epsilon=1e-5, momentum=0.1):
        self.num_features = num_features
        self.epsilon = epsilon
        self.momentum = momentum

        self.gamma = torch.ones(num_features).requires_grad_()
        self.beta = torch.zeros(num_features).requires_grad_()

        self.running_mean = torch.zeros(num_features)
        self.running_var = torch.ones(num_features)

    def forward(self, x, training=True):
        if training:
            # Compute batch mean and variance
            batch_mean = torch.mean(x, dim=0)
            batch_var = torch.var(x, dim=0)

            # Update running statistics
            self.running_mean = self.momentum * batch_mean + (1.0 - self.momentum) * self.running_mean
            self.running_var = self.momentum * batch_var + (1.0 - self.momentum) * self.running_var

            # Normalize
            x_norm = (x - batch_mean) / torch.sqrt(batch_var + self.epsilon)

        else:
            # Normalize using running statistics
            x_norm = (x - self.running_mean) / torch.sqrt(self.running_var + self.epsilon)

        # Scale and shift
        out = self.gamma * x_norm + self.beta
        return out

其中self.momentum用于平滑地更新并跟踪训练数据的运行均值和方差，通常设置为0.9或0.99,有助于减少运行统计数据的批次之间的波动，使得BN在训练中更稳定
在实际的应用或推断阶段，模型通常使用平滑的运行统计数据进行标准化，而不是使用单个批次的统计数据

卷积层

import torch

class ConvBatchNormalizationManual:
    def __init__(self, num_channels, epsilon=1e-5, momentum=0.1):
        self.num_channels = num_channels
        self.epsilon = epsilon
        self.momentum = momentum

        self.gamma = torch.ones(num_channels).requires_grad_()
        self.beta = torch.zeros(num_channels).requires_grad_()

        self.running_mean = torch.zeros(num_channels)
        self.running_var = torch.ones(num_channels)

    def forward(self, x, training=True):
        if training:
            # Compute batch mean and variance for each channel
            batch_mean = torch.mean(x, dim=(0, 2, 3), keepdim=True)
            batch_var = torch.var(x, dim=(0, 2, 3), keepdim=True)

            # Update running statistics
            self.running_mean = self.momentum * batch_mean.squeeze() + (1.0 - self.momentum) * self.running_mean
            self.running_var = self.momentum * batch_var.squeeze() + (1.0 - self.momentum) * self.running_var

            # Normalize
            x_norm = (x - batch_mean) / torch.sqrt(batch_var + self.epsilon)

        else:
            # Normalize using running statistics
            x_norm = (x - self.running_mean.view(1, self.num_channels, 1, 1)) / \
                     torch.sqrt(self.running_var.view(1, self.num_channels, 1, 1) + self.epsilon)

        # Scale and shift
        out = self.gamma.view(1, self.num_channels, 1, 1) * x_norm + \
              self.beta.view(1, self.num_channels, 1, 1)
        return out

Layer Normalization(层归一化)

既然有了BN，为什么还需要LN？

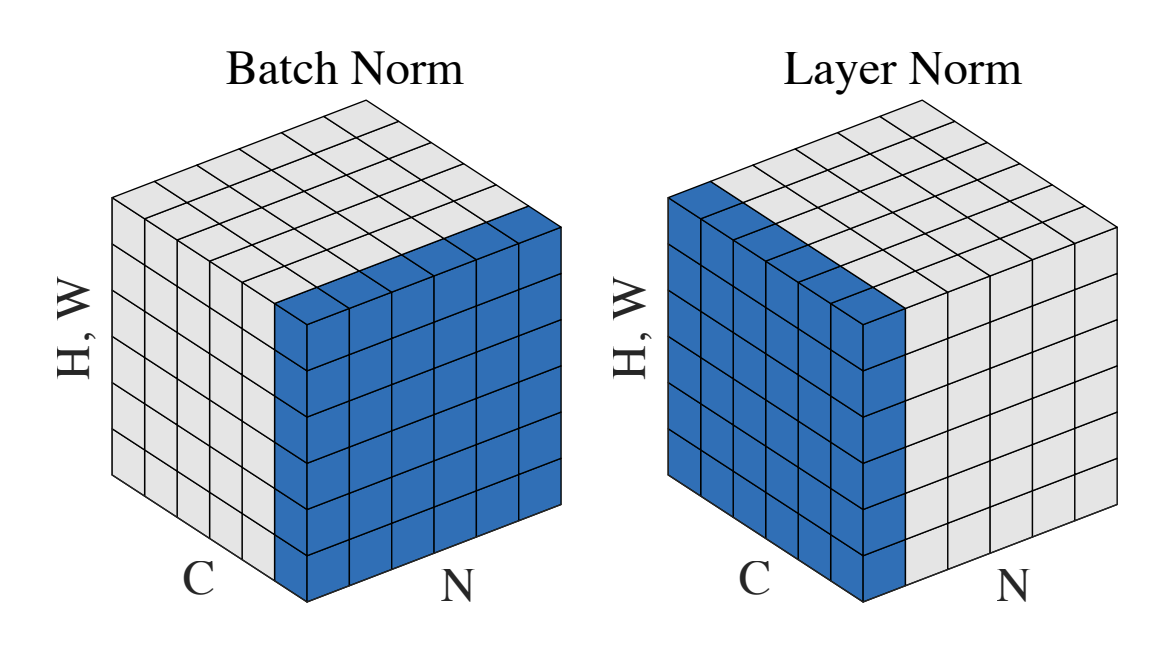
LN与BN的本质不同是normalization的方向不同
- BN是对batch的维度去做归一化，也就是针对不同样本的同一特征做操作。LN是对hidden的维度去做归一化，也就是针对单个样本的不同特征做操作
- 具体而言，BN就是在每个维度上统计所有样本的值，计算均值和方差；LN就是在每个样本上统计所有维度的值，计算均值和方差
在NLP领域，LN更加合适
- 如果将一批文本的作为一个batch，BN的操作方向是将每个相同位置进行scale and shift，而文本的复杂性较高，不同句子的同一位置分布大概率是不同的，因此BN不符合NLP的规律
- 在训练过程中，对BN来说需要保存每个step的统计信息（均值和方差）。在测试时，由于变长句子的特性，测试集可能出现比训练集更长的句子，所以对于后面位置的step，是没有训练的统计量使用的
- 与 BN 不同，LN 是一种横向的规范化，它综合考虑一层所有维度的输入，计算该层的平均输入值和输入方差，然后用同一个规范化操作来转换各个维度的输入

方法

和BN类似，但是normalization的方向不同
输入为一个batch $B$ ，其中每个元素为 $x_i, i \in B$ ，每个元素又有 $|D|$ 个特征
获取单个样本特征均值 $\mu_L$ $μ_{L}$ 和方差 $\sigma_L$ $σ_{L}$
- $\mu_L = \frac{1}{|D|}\sum_{j\in D}{x_{i,j}}$ ， $\sigma^2_L = \frac{1}{|D|}\sum_{j\in D}{(x_{i,j} - \mu_L)^2}$
进行Standardization
- $\hat{x_i} = \frac{x_i - \mu_L}{\sqrt{\sigma_L^2 + \epsilon}}$
- $\epsilon$ 防止除零引入的极小量
进行Scale and shift
- $y_{i} = \gamma \hat{x_i} +\beta$
- 其中 $\gamma$ 为方差(scale参数)， $\beta$ 为均值(shift参数)，均为可学习的参数

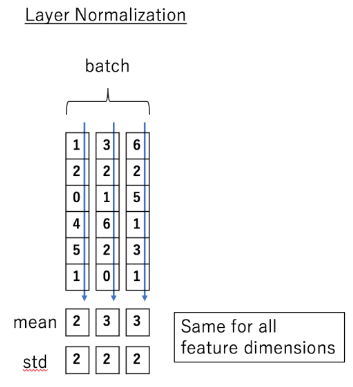
这里可以输入形状[batch, seq_len, dims]看作[3, 6, 1]
图片来自于transformer-illustrated

训练阶段

$\mu_L$ ， $\sigma^2_L$ 对于单个的样本来说都是固定的参数
只需要反向传播时更新 $\gamma$ 和 $\beta$ 即可

推理阶段

推理阶段和训练阶段处理方式其实是一致的
在这个阶段所有参数都是固定的，即 $\mu_L$ $μ_{L}$ ， $\sigma^2_L$ $σ_{L}^{2}$ ， $\gamma$ $γ$ ， $\beta$ $β$ 都是固定值
- $\mu_L$ ， $\sigma^2_L$ 直接根据需要预测的数据计算出来即可
- $\gamma$ ， $\beta$ 在训练结束后，两者收敛，直接采用收敛值即可

作用

LN不依赖于其他数据，不依赖于batch的大小，针对单个数据在其所有特征上进行归一化
LN不需要保存mini-bacth的均值和方差，节省了额外的存储空间

适用场景

mini-batch训练
transformer架构
变长的序列数据的NLP任务
RNN
动态网络场景

缺点

在CNN架构中，特别是图像任务上，LN效果一般不如BN
没有考虑批次信息，LN只对单个数据进行归一化，可能会错过某些和数据总体分布相关的信息
在某些任务中，输入数据的不同特征可能有不同的重要性或规模。由于 LN是在所有特征上进行归一化，这可能会抹平这些特征之间的差异，从而对模型的性能产生负面影响

code

import torch.nn as nn

class LayerNormalization(nn.Module):
    def __init__(self, dims, eps=1e-6):
        super(LayerNormalization, self).__init__()
        self.gamma = nn.Parameter(torch.ones(dims))
        self.beta = nn.Parameter(torch.zeros(dims))
        self.eps = eps

    def forward(self, x):
        # 计算均值和标准差时需要指定最后一个维度
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.gamma * (x - mean) / (std + self.eps) + self.beta

# 使用例子：
ln = LayerNormalization(dims=512)
input_tensor = torch.rand(32, 10, 512)  # batch=32, seq_len=10, dims=512
output = ln(input_tensor)