本文结构和内容主要参考自SivilTaram的博客和chhzh123的博客并加上自己的一些理解

图神经网络

数据常常可以被分类为欧式数据和非欧式数据。
欧式数据通常是我们在日常生活中遇到的最常见的数据类型，例如图像、音频和文本数据，这些数据由简单的序列或网格组成，较为结构化。
非欧式数据不属于传统的固定维度向量空间。例如，社交网络、知识图谱、复杂的文件系统都是非欧式数据。这类数据的关键特点是它们之间的关系不能简单地通过欧氏距离来度量，是非结构化的。

非欧式数据促使了图神经网络（Graph Neural Network, GNN）的出现和发展，GNN中所处理的图一般情况下指的是图论中的图，由若干节点以及连接节点的边所构成的数据结构。

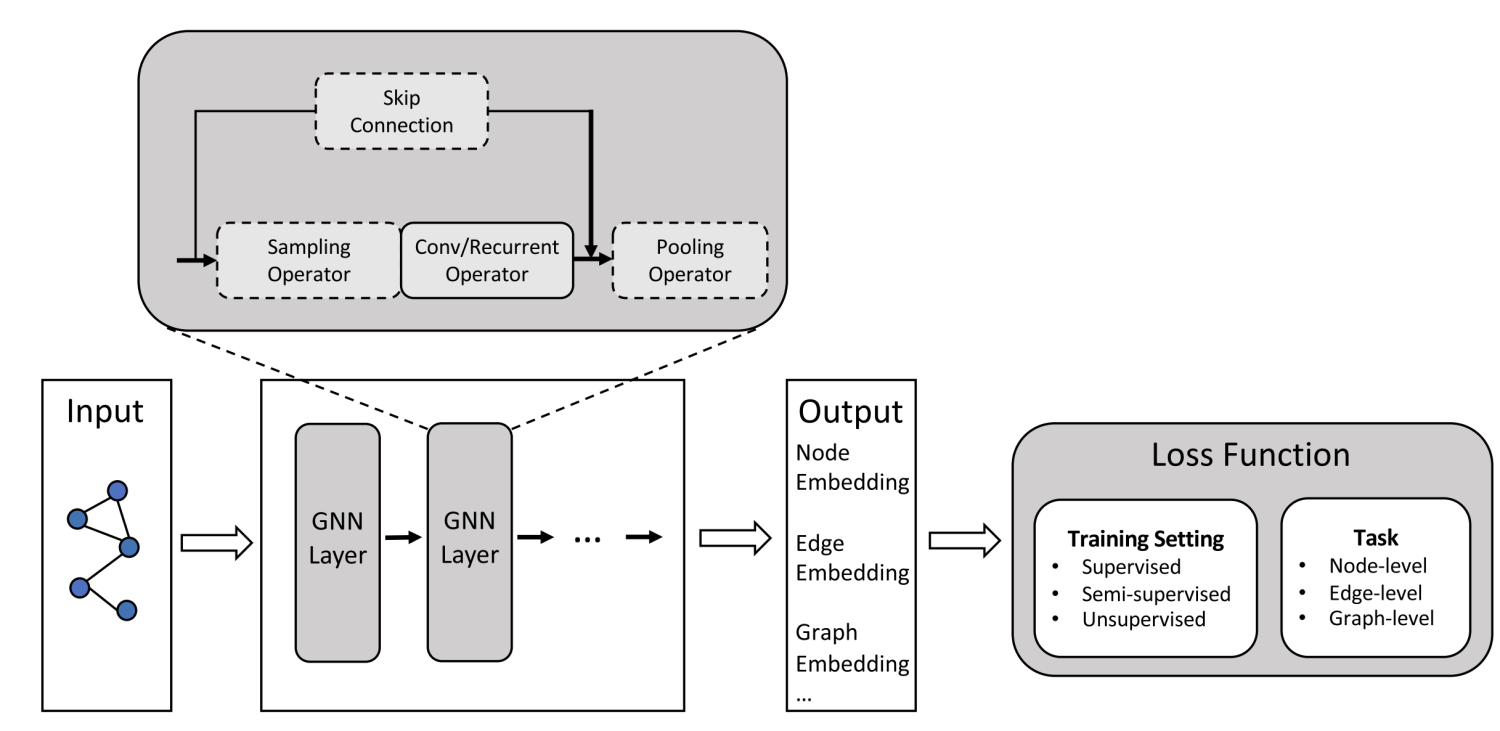
输入：通常为一个Graph Network
输出：节点Label；新的Link；生成新图或者子图

对于图不同的任务

节点层面
Edge(Link)层面 (推荐系统)
整图方面（分子分类），子图方面（导航）

常见的任务

节点分类
Link预测
图分类

原理

给定一组图数据 $G(V, E)$ ，每个节点 $v$ 在图 $G$ 中都有一个关联的特征向量，初始化时，这些特征可以是节点的属性，标签或其他与节点相关的信息，将节点 $v$ 的特征表示为 $h_v$ 。
GNN的基本操作是通过消息传递(Message Passing)来更新节点表示，每个节点从其邻居接受信息，然后使用这些信息来更新自己的表示。
具体来说，每个节点 $v$ 在 $T_{i+1}$ 时刻接受从其邻居 $N(v)$ 在 $T_i$ 时刻产生的信息，并更新其特征表示为:

$h^{T_{i+1}}_v = Combine(h^{T_i}_v, Aggregate(h^{T_i}_{N(v)}))$

$h^{T_i}_{N(v)}$ 是节点 $v$ 在 $T_i$ 时刻的所有邻居特征表示
$Aggregate$ 是聚集函数，用于将所有邻居特征聚合为一个单一的向量
$Combine$ 是组合(or Update)函数，用于将聚合后的邻居特征与自身特征结合在一起
每一个时刻 $T_i$ 共享权重

有了上面公式之后，可以通过迭代消息传递层(GNN Layer)来增加模型的深度，每个节点特征可以通过多跳邻居进行更新，在某种程度上GNN和RNN较为相似。

图卷积

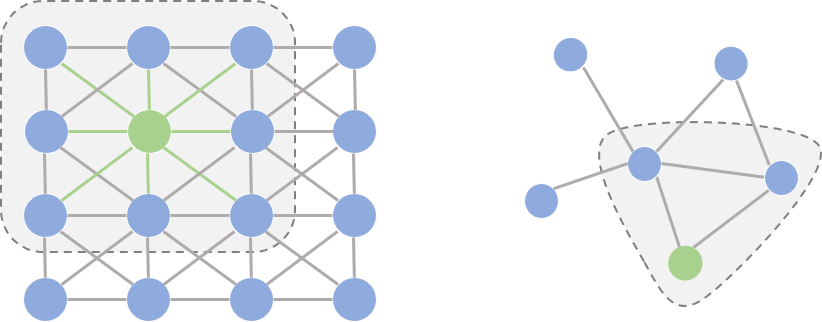
图片来自SivilTaram的博客

将图片中的每一个像素点视为一个节点可以表示为左图，一个普通的图结构可以表示为右图
左侧是一个传统卷积核，右侧是一个图卷积核
可以观察到以左图为代表的欧式空间中，邻居的节点数量都是固定的，但是在右图这种非欧式结构中，节点的邻居数量并不固定，因此传统的卷积核无法适用到图结构中

如何解决邻居节点数量不固定的问题？

将非欧式空间的图转换为欧式空间
找出方法使得卷积核可以从变长邻居节点中抽取特征

图卷积框架

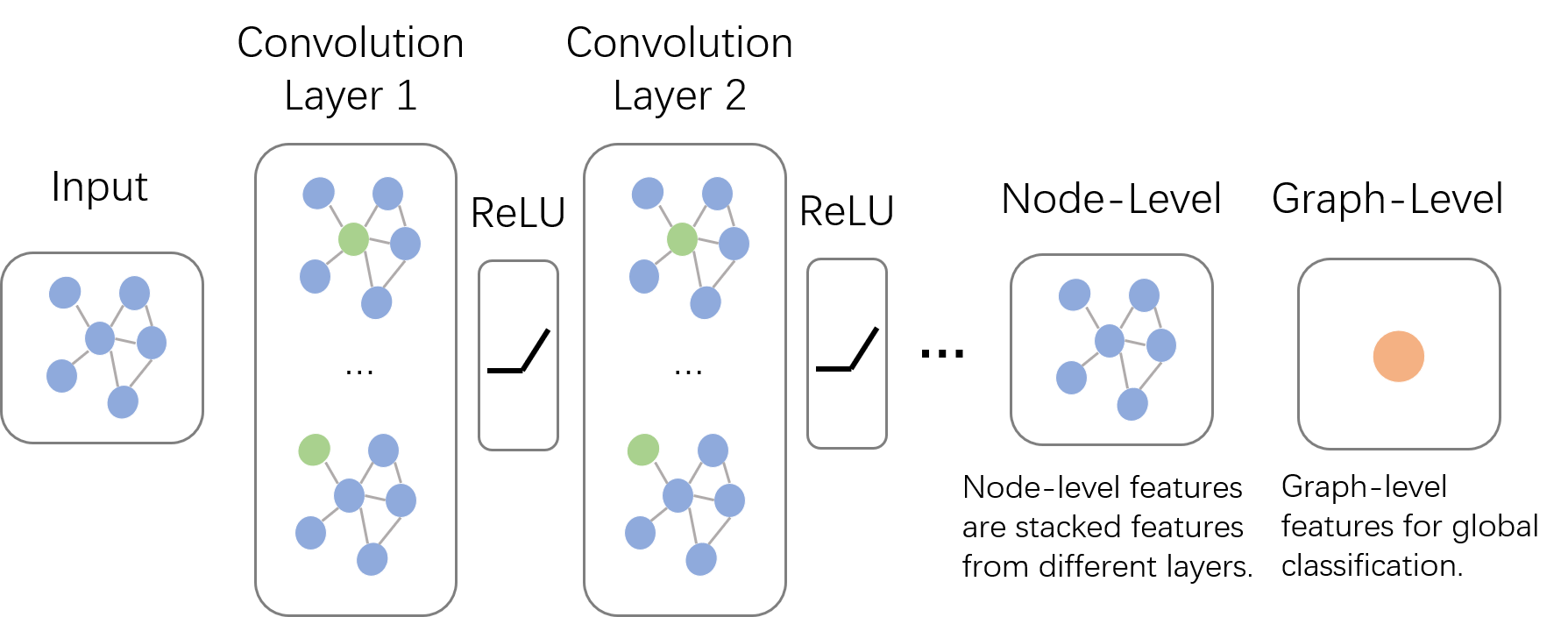
图片来自SivilTaram的博客

输入为一张Graph Network
在每层Convolution Layer中，对每个节点的邻居进行卷积操作(Aggregate)，使用卷积结果更新节点，再经过激活函数如Relu作为输出
以上述操作为一个基本单元，进行Layer的叠加
将最后的输出转换为需求任务进行处理(比如节点分类或者图分类)

GCN对比GNN

GCN与GNN的根本不同在于，GCN是多层堆叠，每一层的参数是不同的，而GNN是迭代求解，每一层的参数是共享的，GNN与RNN结构上比较相似。

空域卷积和频域卷积是图卷积网络中两种主要的卷积方法，下面分别介绍这两种方法。

空域卷积(Spatial Convolution)

基本思想

直接在图上进行卷积，模拟传统CNN中的卷积

工作方式

使用节点的邻居信息，例如节点特征的新值可以是自身特征和邻居特征的加权组合

消息传递模型(Message Passing Model)

这里的消息传递模型和前述GNN中的消息传递为同一内容，这一模型将空域卷积分解为两个过程：消息传递与状态更新，针对GCN重新改写GNN中的消息传递公式：

$h^{l+1}_v = Combine(h^{l}_v, Aggregate(h^{l}_{N(v)}))$

其中 $l$ 代表图卷积的第 $l$ 层，上式的物理意义是收到来自第 $l$ 层每个节点的信息后，根据这些信息来更新自身节点第 $l+1$ 层的状态
在GNN中是根据级联的时间来更新状态，共享参数，在GCN中则是根据级联的层来更新状态，每一层有自己的参数

图采样与聚合(Graph Sample and Aggregate)

在消息传递模型下，卷积操作的对象是整张图的每个节点，意味着需要将所有的节点放入内存或者显存中才能进行卷积操作，对于实际场景下的大规模图，这种方式显然是不可行的。
GraphSAGE(SAmple && aggreGatE)提出的动机就是来解决这个问题，从名字就可以看出来GraphSAGE所执行的操作，先采样(Sample)再聚合(Aggregate)。

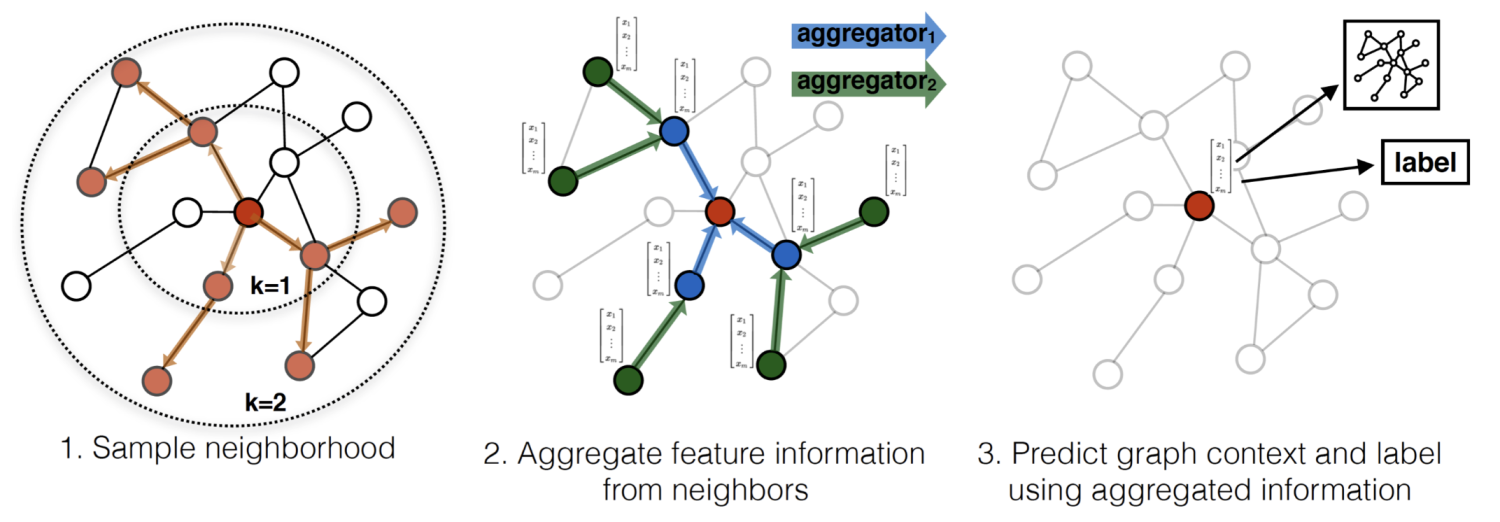
流程

在图中随机采样若干个结点，结点数为传统任务中的batch_size。对于每个结点，随机选择固定数目的邻居结点(这里邻居不一定是一阶邻居，也可以是二阶邻居)构成进行卷积操作的图
将邻居节点信息通过Aggregate函数聚集起来更新刚才采样的节点
计算采样点的Loss，如果是无监督任务，期望图上邻居节点编码相似，如果是监督任务，根据具体节点任务标签计算损失

细化GraphSAGE状态更新公式

$h_ {v}^ {l+1} = \sigma ( W^ {l+1} \cdot Aggregate( h_ {v} ,{ h_ {u}^ {l} }), \forall u \in N[v])$

$W^ {l+1}$ 表示第 $l+1$ 层的权重矩阵
$\sigma$ 表示第 $l+1$ 层的激活函数
从上式可以看出GraphSAGE的设计重点放在了Aggregate函数上，它可以是不带参数的max, mean, 也可以是带参数的如LSTM等神经网络。核心的原则是它需要可以处理变长的数据。

直推式学习和归纳式学习

上一小节的GraphSAGE引入了一个新的概念-归纳式学习(inductive learning)，即通过采样与聚合中心节点的邻居信息来生成节点embedding，这是可以适用于不同graph inputs的(结点或边可以后面再持续插入); 而传统的GNN算法是直推式学习(transductive learning)，即在训练节点embedding时需加载所有节点信息。

频域卷积(Spectral Convolution)

又称谱域卷积，在频域中，图卷积的主要思想是在图的傅里叶空间（或更确切地说，是图拉普拉斯算子的特征空间）中进行卷积。
原公式解释起来比较复杂，可以阅读博客进行理解，这里只介绍由论文化简后的频率卷积计算，一个基本的频域卷积操作可以写为

$\mathbf{H}^{(l+1)}=\sigma\left(\tilde{D}^{-\frac12}\tilde{A}\tilde{D}^{-\frac12}\mathbf{H}^{(l)}\mathbf{W}^{(l)}\right)$

$h^{l}$ 表示第 $l$ 层的节点特征
$W^l$ 表示第 $l$ 层的可训练权重
$\tilde{A} = A + I$ 是邻接矩阵加单位矩阵，单位矩阵是为了加入自循环，这样每个节点也会考虑自己的特征
$\tilde{D}$ 是 $\tilde{A}$ 的度矩阵，即 $\tilde{D}_{ii}=\sum_{j}\tilde{A}_{ij}$
$\sigma$ 是非线性激活函数，如Relu

该公式可以在频域中捕获图上每个节点与其邻居的关系，并利用这些关系来更新节点特征，这种操作也可以多次迭代，每次迭代都会更深入的整合图的信息。
在一般的GCN中实现的就是频域卷积，常见的2层GCN模型代码如下

import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures

# 加载数据集
dataset = Planetoid(root='data/Cora', name='Cora', transform=NormalizeFeatures())

class GCN(torch.nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(GCN, self).__init__()
        self.conv1 = GCNConv(input_dim, hidden_dim)
        self.conv2 = GCNConv(hidden_dim, output_dim)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index

        # 第一层 GCN
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, p=0.5, training=self.training)

        # 第二层 GCN
        x = self.conv2(x, edge_index)

        return F.log_softmax(x, dim=1)

# 定义模型和优化器
model = GCN(input_dim=dataset.num_features, hidden_dim=16, output_dim=dataset.num_classes)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

# 训练模型
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = model.to(device)
data = dataset[0].to(device)

def train():
    model.train()
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

def test():
    model.eval()
    out = model(data)
    pred = out.argmax(dim=1)
    correct = pred[data.test_mask].eq(data.y[data.test_mask]).sum().item()
    return correct / data.test_mask.sum().item()

# 主训练循环
for epoch in range(200):
    train()
    if epoch % 10 == 0:
        test_acc = test()
        print(f'Epoch: {epoch:03d}, Test Accuracy: {test_acc:.4f}')

其他常见模型

GAT(Graph Attention Network)

回忆NLP中的Encoder-decoder模型，由于Encoder需要将一整个句子的信息压缩到一个高维空间向量，再送入Decoder进行解码，这一个高维空间向量的负担将会非常大，因此研究者就考虑让机器学会判断句子中的不同部分的重要性，从而在解码时更加有针对性地获取特征，此即Attention的思想。
将Attention概念引入到Graph中

对于每个节点 $v_i$ ，GAT首先计算该节点与其邻居节点v_j之间的注意力权重，并作归一化得到alpha_ij
使用注意力权重将邻居节点的表示进行加权平均，以更新节点表示
- $h_i^{l+1}=\sigma\left(\sum_{j\in\mathcal{N}_i}\alpha_{ij}Wh_j^{l}\right)$